Publication
Adjustable Constrained Soft-Tissue Dynamics
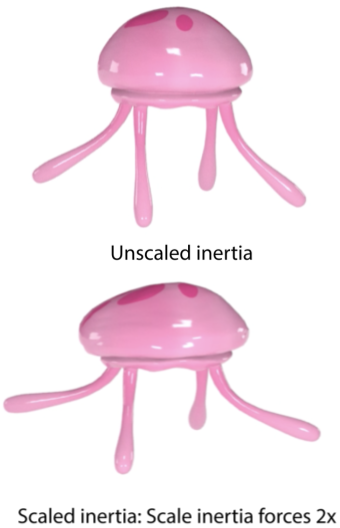
Abstract: Physically based simulation is often combined with geometric mesh animation to add realistic soft-body dynamics to virtual characters. This is commonly done using constraint-based simulation whereby a soft-tissue simulation is constrained to geometric animation of a subpart (or otherwise proxy representation) of the character. We observe that standard constraint-based simulation suffers from an important flaw that limits the expressiveness of soft-body dynamics. Namely, under correct physics, the frequency and amplitude of soft-tissue dynamics arising from constraints (“inertial amplitude”) are coupled, and cannot be adjusted independently merely by adjusting the material properties of the model. This means that the space of physically based simulations is inherently limited and cannot capture all effects typically expected by computer animators. For example, animators need the ability to adjust the frequency, inertial amplitude, gravity sag and damping properties of the virtual character, independently from each other, as these are the primary visual characteristics of the soft-tissue dynamics. We demonstrate that independence can be achieved by transforming the equations of motion into a non-inertial reference coordinate frame, then scaling the resulting inertial forces, and then converting the equations of motion back to the inertial frame. Such scaling of inertia makes it possible for the animator to set the character’s inertial amplitude independently from frequency. We also provide exact controls for the amount of character’s gravity sag, and the damping properties. In our examples, we use linear blend skinning and pose-space deformation for geometric mesh animation, and the Finite Element Method for soft-body constrained simulation; but our idea of scaling inertial forces is general and applicable to other animation and simulation methods. We demonstrate our technique on several character examples.
Our results:
